そのプログラム、正しく書けている?「形式検証」入門 :第二回
形式検証に関連するコラム「形式検証」入門の第二回を掲載いたします。
今回の内容は、弊社が代理店をしているAdaCoreのパートナー企業であるニルソフトウェアの代表者、伊藤様に作成いただきました。
第二回 形式検証とは
前回は,Ada言語の紹介でした.今回は,形式検証について,説明したいと思います.
形式検証とは,“数学的なモデルを用いて,作られたプログラムが仕様と合っているかを確認する”ことだと前回説明しました.
今回は,形式検証のしくみについて簡単に説明します.但し,形式検証には,様々な技術があります.ここでは,SPARKで利用している技術が中心になります[1].しかし,その技術は,最も一般的なものです.
もちろん,SPARKツールを用いて形式検証をするときに,詳細な知識は必要ではありません.しかし,知っていることでより高いレベルで形式検証できるようになります.
形式検証技術は,大きく2つに分かれます.一つは,モデル検査というふるまいの検査を行う技術です.示したい性質を,時制論理式で記述します.有限状態機械をイメージすると分かりやすいと思います.例えば,「いつかはSwという状態に遷移する」という仕様作成者が望んでいる性質(liveness)を,有限状態機械が持っているかを知りたい.このときに,起こり得る状態遷移を網羅的に調べることで,その性質があるかどうかを確認するという方法です.
もう一つの方法は,証明器を用いた検証です.プログラムが望ましい性質(それは記述しなくてはなりません)を,持っているかを,証明しようと試みます.今回の対象は,後者になります.
■ プログラムから形式検証への流れ
最初に,SPARKでの形式検証の流れを示します[2].図1を見て下さい.
ここには,SPARKでのツール間のデータの流れを示しています.まず,SPARK のコードは変換され,Why3に渡されます.Why3では,各証明器に対して,VC(検証条件)を発行します.無事に証明ができれば,充足している(sat)と返ってきますし,充足していない場合は,充足していない(unsat)が,可能ならば反例と共に答えとして返ってきます.
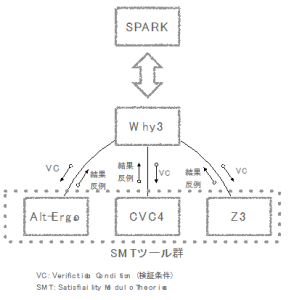
図1. SPARKにおける証明器の利用
図中の,Alt-Ergo/CVC4/Z3は,SMT (Satisfiability Modulo Theories) 証明器と呼ばれるものです.SMTについては,のちほど説明します.SPARKでは,製品版とコミュニティ版で,この証明器の組み合わせが,少し違います[1].
表1.SPARKで標準でインストールされる証明器

複数の証明器がインストールされている場合,どの証明器を使うかを,設定により指定することができます.また,適切なVCを生成するようにすれば,Why3がサポートしている範囲(文献[5]に完全なリストがあります)から,証明器を選ぶことができるようになります.
■ Hoare の 3 つの組
最初のステップは,検証条件(VC)の生成です(図1).その説明のために,最初にHoareの3つの組について紹介します.
有名な Hoare の 3 つの組[4]とは,以下です.
![]()
対象とするプログラムは,命令の列としての I です.P,Qは,(述語論理で云う)述語です.それぞれは,事前条件と事後条件に対応します.読み下すと,事前条件 Q が成立していれば(真であれば),プログラム I によって,事後条件 R が成立する(真となる)となります.プログラムの一番基本的な形です.
いま,最弱事前条件(weakest precondition)を考えます.記号としては,述語変換子wp を用いて,次のようになります.これは,プログラムが有限時間内に実行を終了し,Qを満たす状態になる,そのような全ての事前条件を指します.
![]()
ここでの証明とは,次が成立することを示すことです.
![]()
即ち,最弱事前条件Pが成立するならば,プログラムIによって,必ず,事後条件Qが成立するということです.即ち,そのような最弱事前条件を求めることができ,常に維持されているならば,書かれたプログラムIが,Qに到達することを示せます.これが図1のVC(Verification Conditions:検証条件)になります.
この計算のために複数のルールがありますが,例えば,次のルールから,最弱事前条件を求めて見ます.
![]()
このルールを,下記に適用します.まだ,事前条件は分かっていません.
![]()
先の「代入に関するルールを適用します.Eに相当するのは,x+2ですから,次のように変形できます
![]()
ここから,直ぐに次を得ることができます.
![]()
もちろん,事前条件が,x>=4でも,プログラムを適用した結果,事後条件を満足します.しかし,上記の操作により,もっとも広い範囲 x>=3 を得ることができます.これが,ここでの「最弱」の意味になります.
証明とは,P が,最弱事前条件に対して,P⇒wp(I,Q).即ち,P⇒x≥3といえれば良いわけです.従って,これが証明すべき条件となります.
但し,実際には,検証条件は,上記を否定したものを証明器にかけて,制約を充足するかどうかを調べます.
否定した式を充足しない,即ち,満足する値の組を持たないということは,元の検証したい式が成立していることになります(否定になるような値の組が存在しないのですから).
一方で,否定した式が成立する場合があるというのは,元の式が常に成立するわけではないということになります.この値の組は,その反例となります.
さて,次の問題は,様々な式がある中で,充足する値を持つか否かを,どうやって見つけるか,ということになります.これは,制約充足問題の解決法として,最近非常に発達した分野になります.最初に,SATと呼ばれる技術を,次に SMT と云われるプログラムの形式検証に用いる技術について簡単に説明します.
■ 充足問題解決:SAT
SAT という名前は,充足可能性を示す Satisfiability の英語先頭3文字をとっています.命題論理式を対象として,充足可能性を調べます.充足可能性とは,真となる値の組み合わせがあるかないかを指します.
最初に,命題論理式(の組)を,連言標準形CNF(Conjunctive Normal Form)と呼ばれる形式に変換します.例えば,以下の形です.
![]()
∧ が連言(ソフトウェア技術者にとってなじみのある言葉では論理積)になります.P, Q は命題です.連言でつないでいるので,
P, Q が共に True の時に成立します.
少しだけ複雑なCNFの例は,以下です.
![]()
全体は,連言で接続されています.それぞれを節と呼びます.節の中にある,各(原子)命題はリテラルと呼びます.先のリテラル(ここでは節でもあります),P, Q は,新たなリテラル P1,P2と 或いは Q1,Q2 からなる節を選言(論理和)でつないだものとなっています.
SATでは,次のようにして,充足可能性を調べます.以下の例とともに説明します[注].
*注:ここでの例は,CVC4 の開発者の一人Andrew Reynolds氏の例に基づきます.とても分かりやすい説明になっています. (http://homepage.divms.uiowa.edu/~ajreynol/pres-dpllt15.pdf)
![]()
この式は,既に連言標準形になっています.最後のリテラルは単一ですので,B は False になります(Trueだと,たちどころに上記論理式は,成立しなくなります).[A1]最初の節 A ∨ B は,True になる必要があり,かつ B は False なので,A は,True です.[A2] 節 (C ∨ D) は何もヒントとする情報がないので, C を True と仮定します [A3].これにより全ての節は True になります.矛盾は生じていないので,この式を充足していることが分かります.また,成立する組は,A : True, B : False, C : True です.もちろん,他にも充足する組はありますが,充足する組があるということは分かったわけです.
■ 充足問題解決: SMT
SMT は,Satisfiability Modulo Theories の略になります.硬く訳すと,理論を法とする充足可能性(解決)であり,この問題を解くツールのことを,SMT ソルバと呼びます.理論を法と訳しましたが,使用する理論は単一ではなく,様々な理論があります(英語では,複数形になっていることに気がつくでしょう).ツールによって使用する「理論」の種類は異なります.一般には表2に示す理論を持っています.
表2. 一般にSMTで用いられる理論

SAT では,命題のみを扱います.先の例のように,命題 P の真偽だけを問題にしています.命題P が具体的に何を示すかは気にしません.SMT では,更に表現力がある一階述語論理を扱います.いまは,プログラムの形式証明を考えています.従って,利用するのはSMT ということになります.もちろん,SMT も SAT 技術の上にあるので,正確には両者によって,形式検証が可能になります.
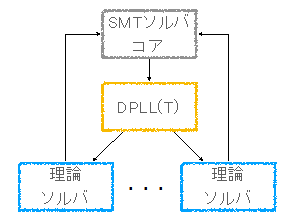
図2 SMTソルバの基本的な構造
ツールは,SMTソルバと呼ばれ,その構造は図2のようになっています.
SMTソルバは,適切な理論ソルバを選択しながら,充足問題を解いていきます.DPLL というのは,SAT で標準的に使われるリテラルの選択方法です.SATのところで見たように,矛盾に出会ったときには,最後の仮説に戻り,異なる値で再実行します.SMTでは,更に論理Tも選択するので,DPLL(T) という名称で呼ばれています.
さて,例を見てみます.
![]()
変数は全て整数とします.線形演算がでてきますから,表2にあるLIA(Linear Integer Arithmetic) を使います.
いま,扱いやすいように,各不等式を命題で置き換えます.即ち,各不等式をリテラルとして表現することになります.
![]()
得られた(5)は,SATの説明であった(3)と全く同じかたちをしています.
従って,途中までは,SATと同様に考えることができます.SATの時に,適用した仮定 [A3] は,C: True でした.また,最終的に得られた,充足する組は,A : True, B : False, C : True です.
しかし,命題の場合は良いとして,本当にこの組を取り得るのかを考える必要があります.各命題の実体は不等式で,そこに出てくる変数間には,関係があるからです.
![]()
いま整数で考えています.A:True,C:True ですが,明らかに,そのような整数x は存在しません.ツールでは,理論ソルバ TLIA がこの矛盾を見つけます
さて,このあと,DPLLに従い,バックトラックすることになります.図2に示すとおり,理論ソルバから,SMTソルバコアに戻り,再度,DPLLが動作します.その結果,最も直近の仮定に間違いがあったと考えます.即ち,最後に選択した仮定[A3]でC: Trueとしたことが間違っていたと考えます.
従って,仮定を見直すことになります.また,いま見つけたことは,有益な情報ですから,元の論理式に付け加えることにします.AとCは同時にTrue になることはない,即ち,¬(A ∧ C) ⟺ ¬A ∨ ¬Cです.新しい式は,次になります.
![]()
C: True で矛盾が生じたので,新しい仮定は,C: False になります.ここから,必然的に,2番目の節(C ∨ D)がTrueの必要があり,D: True がでてきます.D は,x + y > 4の置き換えでした.これが True ということです.ところで,BはFalseでした.B 即ちx + y >0との関係を考えると,矛盾があることが分かります.
ここでも同様に新たな節を付け加えます.
![]()
さて,更にバックトラックして,仮定を見直したいのですが,もともと仮定を置いたのは,一箇所だけでした.既に,その仮定は真偽ともチェックしました.もうできることはありません.結果として,この論理式は,充足していない (unsat) ということになります.
SAT と定理により,協調して充足問題を解決しようとしているところが,興味深いアプローチになっています.
次に,SPARKツール で,どのように定理証明を行うかを簡単に見てみます.
■ SPARKで証明
簡単なSPARK言語の例を見てみます.SPARKについては,次回の説明ですが,基本的には前回説明したAda言語の構文と同じです.

図3-1 仕様部
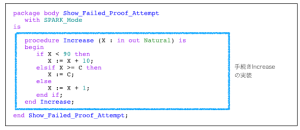
図3-2 ボディ部
手続きIncrease において,ボディ部の実装は,仕様部にある事後条件を満足しているでしょうか.仕様部にあるように,自然数型 C が 100 であれば,問題なさそうです.いま,85を入力すると,Xは,95となります.これは,事後条件の最初のガード条件にヒットし,X>X’Old を満足します.では,定数Cの値を含めて,手続き Increase を安心して使うことができるでしょうか.
SPARKの処理系(gnatprove)を用いて,簡単に確認することができます.SPARKのIDEであるGPSを使ってみましょう.
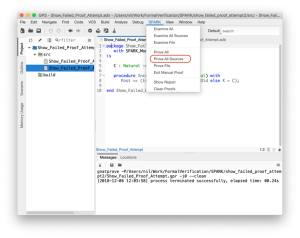
図4-1 GPSで,SPARKメニューを開いたところ
SPARKメニューから,”Prove All Sources …” を選択します.詳細設定用のダイアログパネルがでますが,気にせず “Execute” ボタンを選択します[注].
*注:この詳細画面で,証明器(SATソルバ)を変更することができます.その他各種の設定が可能です.
直ぐに答えは返ってきます.
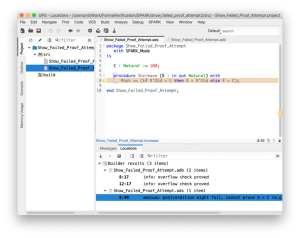
図4-2 GPSでの証明結果の表示
後の行は,次のようなメッセージです.

このメッセージは,仕様部の8行目で,事後条件を満足しない場合があることを示しています.例えば(e.g.) のあとにある,CとXの値が,満足しない例,即ち反例を示しています.
ちなみに,ボディ部の2つのInfo(8行目,12行目)は,オーバフローが発生していないことを示しています.
表明を使うことで,どういう性質を持てば良いかを示すことになります.いったん必要な記述をしておけば,あとは,ボタン一つで,証明を行うことができます.
なお,このプログラムは,AdaCoreの学習用サイトにあるものです[6].このサイトで,実際にSPARKをインストールしなくても,証明を試してみることができます.
■ まとめ
今回,形式検証で実際に行われていることを簡単に説明しました.
ユーザとして見た場合,覚えておいた方が良いことを最後に書いておきます.
今回は明示的な表明記述に対して,それが維持されるかどうかを証明するというところに重点をおきました.しかし,実行時に見つかる次の点も,(特別な表明がなくても)証明器によって見つけることができます.
- 配列添字の範囲検査
- ゼロ割り
- オーバフロー
一方で,証明ができない場合もあります.それは,証明器が(SMTの)理論に依存しているからです(証明器については,表2を見て下さい).例えば,非線形の問題(かけ算,モジュロー演算,累乗等)は,扱うことができません.
いつもの言い方ですが,形式検証によって,プログラムの多くの箇所を確認できます.それでも残る部分は通常あり,テストが必要となります.しかし,全体としてみれば,より効率的に検証が可能になります.
また,Coqのようなインタラクティブな証明器を使うことで,更に,形式検証の範囲を広げることも可能です.
(NIL 伊藤昌夫)
Reference
[1] AdaCore, SPARK 2014 User’s Guide 20.0w, https://docs.adacore.com/spark2014-docs/html/ug/en/appendix/alternative_provers.html#alternative-provers
[2] Jackson, Paul B., and Grant Olney Passmore. “Proving SPARK verification conditions with smt solvers., ” http://homepages.inf.ed.ac.uk/pbj/papers/vct-mar11-draft.pdf (2009).
[3] BIERE, Armin; HEULE, Marijn; VAN MAAREN, Hans (ed.). Handbook of satisfiability. IOS press, 2009.
[4] GRIES, David. The science of programming. Springer Science & Business Media, 2012. (日本語訳:D. グリース著/筧捷彦訳,プログラミングの科学,培風館, 1991, 最弱事前条件については,7章に説明があります)
[5] http://why3.lri.fr/#provers
[6] https://learn.adacore.com/ (”Courses” の “Introduction to SPARK” に様々な例があります)

